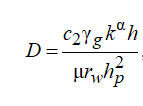В работе приведен алгоритм для расчета притока газа к горизонтальной скважине с учетом потерь в стволе, более точно учитывающий процессы в системе пласт-скважина, чем большинство стандартных моделей. Для этого использованы известные уравнения в нестандартном наборе. Также предусмотрена возможность исследования влияния различных пластовых и скважинных параметров на дебит горизонтальной газовой скважины путем численного расчета производных. Для реальной скважины даны определенные рекомендации по учету данных параметров с точки зрения дебита, а также приводятся соображения по подбору оптимальной длины ствола и оценке необходимой точности в определении проницаемости и анизотропии для целей расчета дебита.

Ключевые слова: дебит, газ, горизонтальная скважина, моделирование, проницаемость, пласт, вязкость, плотность.

 

Существуют различные постановки задачи о притоке газа в скважину. Далее в работе используется постановка Joshi, в которой уравнение притока для дебита горизонтальной газовой скважины при псевдоустановившемся режиме притока выглядит следующим образом 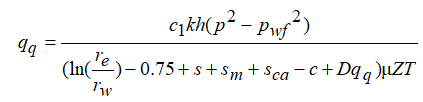[1]:

 

                                                (1)

где q_g -дебит газа; p — среднее пластовое давление; p_wf — среднее забойное давление; s — отрицательный скин, зависящий от длины горизонтальной скважины; s_m — механический скин, s_ca — скин-фактор, зависящий от формы дренируемой области; c — константа, зависящая от формы дренируемой области; k – проницаемость; h — толщина пласта; r_e — радиус дренирования;

r_w — радиус скважины; Z — сжимаемость газа  в пластовых условиях, α – показатель степени, зависящий от типа коллектора; T — пластовая температура; µ — вязкость газа; β— коэффициент фильтрации при высоких скоростях; γ_g — относительная плотность газа; h_p — перфорированный интервал; k — проницаемость в призабойной зоне; с₁, с₂ – константы, зависящие от используемых единиц.

В работе[2] представлено решение для расчета дебита горизонтальной скважины с учетом потерь давления в горизонтальной секции ствола скважины. Для ламинарного потока это решение имеет вид:

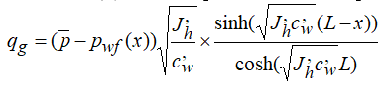(2)

где — продуктивность горизонтальной скважины на единицу длины; c_w^’=c₃µ/d⁴— коэффициент потерь давления в стволе скважины; p_wf(x)- забойное гидродинамическое давление в точке x; x— расстояние, замеренное вдоль ствола скважины от башмака скважины; q_g— продуктивность скважины в любой точке вдоль ствола; L — длина горизонтального ствола скважины; d — диаметр ствола; c₃— константа, зависящая от используемых единиц.

Основная идея состоит в том, чтобы решать совместно уравнение притока к скважине из пласта и уравнение течения газа в стволе. Это возможно сделать лишь численными методами. В этом случае возможно рассчитать дебит горизонтальной скважины с учетом потерь на трение в стволе. Это предлагается сделать следующим образом. Ствол скважины разбивается на элементарные секции и считая, что вдоль каждой такой секции пластовое давление остается постоянным, а также при допущении того, что приток осуществляется только с одного конца секции (противоположного тому, где задано забойное давление) к ней применяется формула притока из пласта. Затем, зная приток из пласта, по формуле (2) рассчитывается давление на конце секции, из которого идет приток. Затем итеративно процесс повторяется для каждой элементарной секции, в результате забойное давление для каждой секции является своей расчетной величиной и нарастает по направлению к башмаку скважины. Коэффициенты сверхсжимаемости, вязкости, зависящие от давления, принимаются для каждой секции отдельно, что позволяет смоделировать поток в скважине с учетом изменения свойств реального газа. Общий дебит горизонтальной скважины затем рассчитывается суммированием по всем секциям. При этом вдоль каждой секции допустима различная проницаемость и мощность пласта, а также все остальные параметры, входящие в уравнение притока.

Согласно описанному алгоритму был составлен расчетный код на С++, который являет собой кусочно-неоднородную модель притока газа к горизонтальной газовой скважине с учетом трения в стволе.

Отметим, что уравнение (2) применимо лишь для ламинарного течения, для турбулентного режима притока модель будет сложнее. Принимая во внимание, что проблема турбулентности потока не так часто проявляется для горизонтальных скважин, в отличие от вертикальных, далее везде подразумевается, что поток газа ламинарен.

Также в процессе анализа производительности скважины зачастую необходимо оценить степень влияния того или иного параметра, входящего в уравнения (1)-(2). Для этого программный код был дополнен возможностью нахождения производных дебита по интересующим параметрам.

Далее рассматривается реальная скважина со следующими параметрами: проницаемость – 30 мД, анизотропия – 0.1, толщина пласта -10м, длина ствола горизонтального участка скважины – 200 м, радиус контура питания – 600 м, радиус скважины 0.07 м, относительная плотность газа 0.64, вязкость – 0.014 сп, пластовая температура – 284 K, устьевое давление -102.81 кгс/см², пластовое давление -126.46 кгс/см². Рассчитанный дебит по описанной методике составляет 88 тыс.м³ газа в сутки.

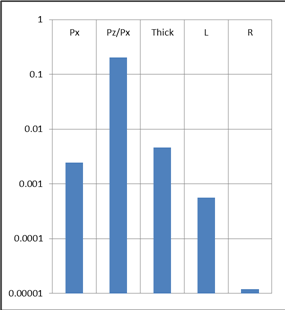
На рис.1 показана гистограмма всех параметров, влияющих на дебит скважины, по вертикальной оси – максимальная производная, полученная при соответствующем исследовании. В используемых единицах максимальное влияние на дебит оказывает анизотропия (д.ед.), следом идут толщина (м) и проницаемость (мД), затем длина горизонтального участка скважины (м) и, наконец, радиус контура питания (м).

Рис.1 Чувствительность дебита к различным параметрам притока

На влиянии длины ствола горизонтальной скважины на дебит газа следует остановиться более подробно, поскольку этот параметр является техногенным, во многом зависящим от применяемой технологии и может быть заранее известен [3,4].

На рис.2 (слева) приведен дебит горизонтальной скважины в зависимости от длины ствола, а также его производная по длине. Заметно, что после 300м производная выполаживается, что означает весьма низкую степень влияния дальнейшего увеличения длины на дебит. Если известна стоимость затрат на каждый дополнительный метр проходки, с помощью подобного графика легко оценить целесообразность увеличения длины скважины. Рис.2 (справа) иллюстрирует зависимость подобных производных от проницаемости пласта. Заметно, что длина ствола оказывает гораздо более существенное влияние на дебит при малой проницаемости, чем при большой. Поэтому столь важно бурить более длинные стволы именно в низкопроницаемых коллекторах.

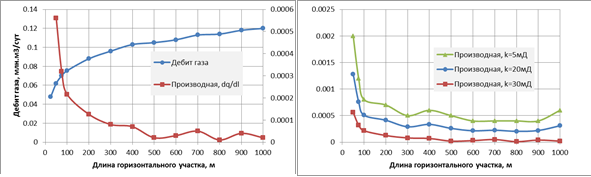Рис.2 Зависимость дебита от длины горизонтального участка (слева)

Таким образом, разработан численный метод решения задачи притока к горизонтальной скважине с учетом потерь давления в стволе, а также численно исследовано влияние различных параметров на дебит горизонтальной газовой скважины. Даны рекомендации по оценке и учету различных пластовых и скважинных параметров с точки зрения определения начального дебита скважины. Подобные оценки будут полезны как при выборе оптимальной траектории скважины во время бурения, так и при дальнейшей эксплуатации [5].

Список литературы

1. Joshi S.D. Horizontal Well Technology, Penwell Publishing Company Tusla, USA, 1991.

2. Dikken B.J.: Pressure Drop in Horizontal Wells and its Effects on their Production Performance // JPT (Nov. 1990)

3. Griffith, P. 1984. Multiphase Flow in Pipes // JPT 36 (3): 361-367. SPE-12895-PA.

4. Giannesini J. F. Production Technology Takes New Direction for Horizontal Wells // World Oil. May, 1989.

5. Алиев З.С, Шеремет В.В. Определение производительности горизонтальных скважин, вскрывшие газовые и газонефтяные пласты, М.:Недра, 1995.

Курганов Дмитрий Владимирович, к.ф.-м.н., доцент, kourganov@rambler.ru, Россия, Самара, Самарский государственный технический университет им.В.В.Куйбышева

SENSITIVITY OF THE HORIZONTAL GAS WELL PERFORMANCE IN RESPECT TO SOME RESERVOIR PARAMETERS

 

Kurganov D.V.

 

Horizontal well performance, including gas wells productivity, has been widely explored by domestic and foreign engineers. Horizontal well technology nowadays is the most powerful and complicative tool for development of oil and gas reservoirs. The cost of horizontal drilling permanently declines (comparatively to the previous century) so it is spread widely all over the globe.

Mathematical models of horizontal well are much more complicative then common slanted and vertical wells. In this paper special algorytm proposed for calculation of the gas inflow into horizontal well taking into account pressure losses in well itself. Also by calculating derivatives there is sensitivity of gas rate to several reservoir and well parameters investigated. Those parameters are permeability, thickness, well length, anisotropy etc.

For the real field well some practical recommendations are given in respect to permeability determination and estimation of reservoir parameters.

Keywords: rate, gas, horizontal well, model, permeability, reservoir, viscosity, density.

Kurganov Dmitri Vladimirovich, PhD, Ass.prof., Kourganov@rambler.ru, Russia, Samara State Technical University.